椭圆曲线和椭圆其实是两种不同的东西,它是指满足特定方程的平面上的点的集合。之所以带上“椭圆”二字,是因为人们在计算椭圆周长引出椭圆积分,第一类椭圆积分的反函数引出椭圆函数,椭圆函数可以参数化为非奇异三次代数曲线,有理域上的非奇异三次代数曲线被取名为 椭圆曲线。
一、椭圆曲线方程及图像
$$y^{2} = x^{3} + a*x+b$$
其中,要求曲线是非奇异的 (处处可导),则有 $4a^{3}+27b^{2} {\kern 5pt}!= 0$ 。方程中 a 与 b 的取值是实数范围,随着两个值的变动,其图像大致如下,可以看到椭圆曲线是关于x轴对称:

二、定义在椭圆曲线上的运算
2.1 加法运算
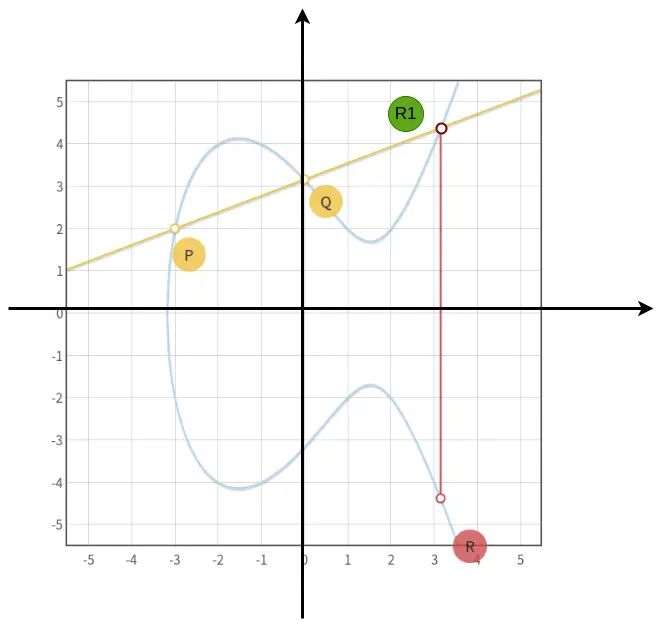
在椭圆曲线上定义两个点 $P$ 和 $Q$,连接两点使得所得直线与椭圆曲线相交于 $R1$ 点,过 $R1$ 点做 $x$ 轴垂线交椭圆曲线于 $R$ 点,由椭圆曲线的性质可知 $R1$ 点与$R$ 点对称,同时我们可以得到椭圆曲线的加法运算:
$$P+Q = R$$
同理连接 $P$ 点和 $R$ 点,交椭圆曲线于 $R2$ 点,同样过 $R2$ 点做 $x$ 轴的垂线交椭圆曲线于 $H$ 点,如下图所示:
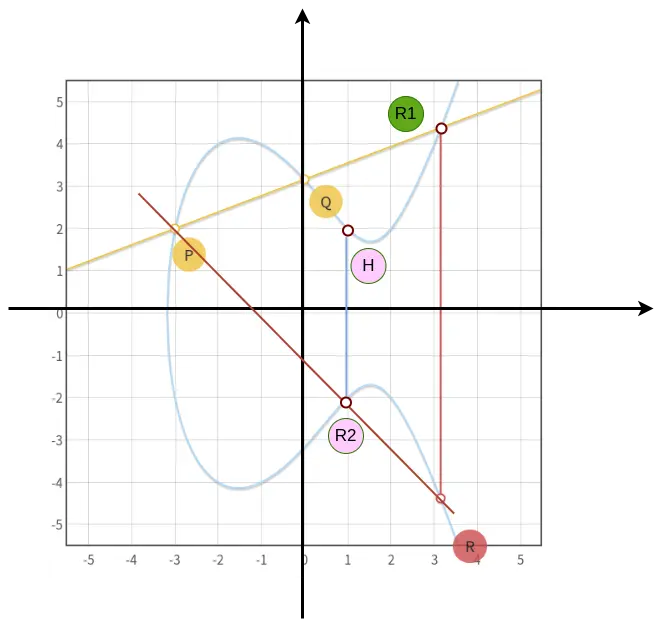
这样继续连接 $P$ 点和 $H$ 点…就可以得到如下过程:
$$P+Q = R \\ R+P = H \\ H+P = …$$
2.2 乘法运算
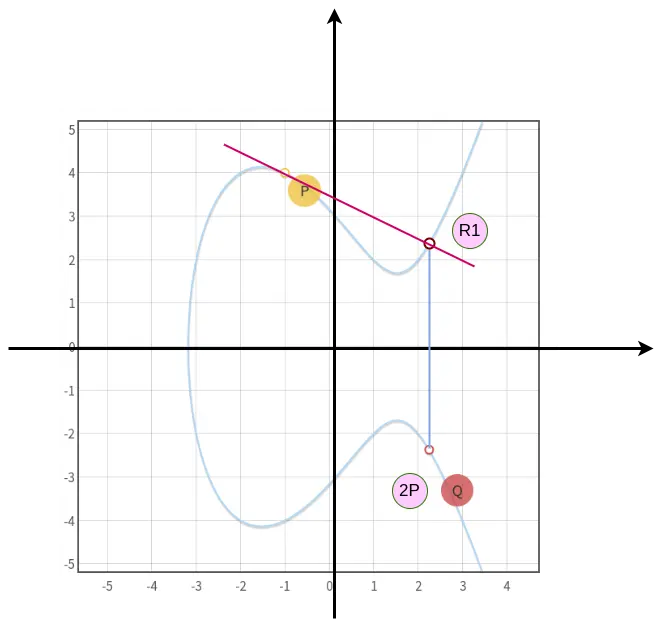
如图所示,过 $P$ 点做切线(因为要保证椭圆曲线上的每个点都有切线,所以限定$(4a^{3}+27b^{2} {\kern 5pt}!= 0)$),交椭圆曲线于
$R1$ 点,同样过 $R1$ 点做 $x$ 轴垂线交椭圆曲线于 $Q$ 点,这样我们认为在这种 切点 情况下加法运算为 $P + P = 2P$ ,即 $Q$ 点为 $2P$ 。同样在 $2P$ 点做切线,我们可以得到 $4P$ 点。而不在通过 $3P$ 的结果来寻找 $4P$ 。如此引入 $P+P$ 的概念可以极大的降低运算次数,帮助我们快速寻找到要找的点。例如我们想得到 $1029P$ ,该怎么做呢?
$$1029P = 1024P+4P+1P \\ 1029P = 2^{10}P+2^{2}P+2^{0}P$$
这样一共需要计算12次即可得到 $1029P$ 的结果。
2.3 性质说明
椭圆曲线密码ECC是椭圆曲线在 ElGamal 体系下的应用,ElGamal 体系就是定义在群上的,那么同样的在椭圆曲线上的一些运算需要具有 “群”的性质:
- 封闭性,定义在椭圆曲线上的点的运算结果肯定还在椭圆曲线上,要么就是无穷远点。
- 结合律,满足,三点共线并没有规定顺序,所以(P+Q)+R=0=P+(Q+R)
- 单位元,就是无穷远点0,每个点加无穷远点还等于这个点
- 逆元,每个点的逆元肯定存在,因为椭圆曲线关于 x 轴对称
三、椭圆曲线算法与数字签名
为什么说椭圆曲线可以用来做数字签名呢?我们知道判断某种方法是否适用于签名或者加密的前提是对于正向操作是容易的,而对于是逆向操作是无法实现的或者说实现起来是非常困难的。如下图所示:
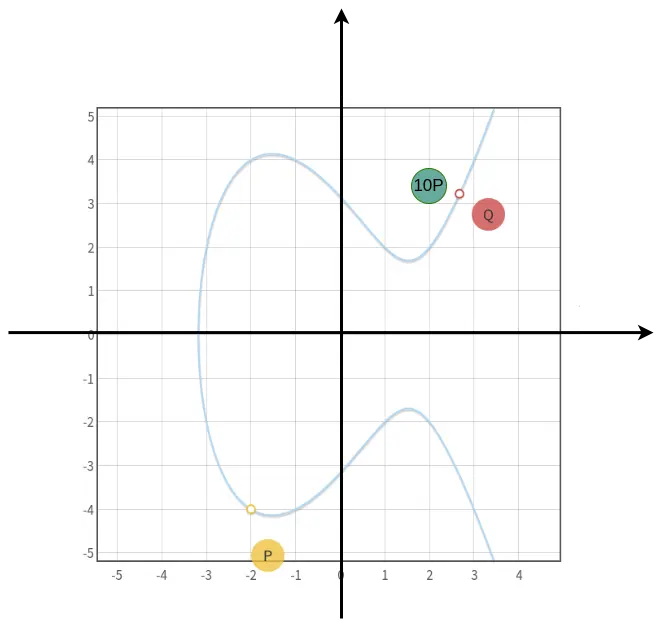
选定 $P$ 点,在经过10次相加后得到 $10P$ 的位置,即 $Q$ 点。如果在不知道经过几次相加,只知道 $Q$ 点的位置的情况下: $Q = k*P$ ,想通过 $k = Q / P$ 的方式来计算 $k$ 是无法实现的($P,Q$均为坐标点)。简单打比方说,我在一个房间前门开始踢球,踢了一段时间之后球落在房间的某个位置,这时让你来回答我踢了多少次才将球踢到这个位置?对于你来说,能做的方法就是从前门开始将球向房间的各个方向踢一点一点的尝试。我们从这个例子中可以看出对于我来讲,踢球是简单的,但是回答踢了几次是困难的,所以这符合签名或加密的要求。
回到上图中的问题,我们无法通过直接计算来确定 $K$ 的值,只能通过比较来做:
$$2P == Q {\kern 10pt} \times \\ 3P == Q {\kern 10pt} \times \\ ….. \\ 10P == Q {\kern 10pt} \surd $$
这样最终确定 $k$ 的值是10。那么如果这个 $k$ 的值非常大呢?比如:
$$k = 0X9FAB78D58CA825723781EFA98A5BD235F1C$$
$Z = K*P$ ,此时如果再一个一个的计算是非常费时的,因此在非对称加密算法中,将一个非常大的数$K$作为私钥,而将$K*P$得到的$Z$点作为公钥分发出去。限于算力的影响是无法推算出$K$的。
现在我们以实际应用中的曲线来做说明:在椭圆曲线方程中取 $a=0,b=7$ ,是比特币所使用的曲线 $secp256k1$ :
$$y^{2} = x^{3}+7$$
在比特币中,选择的初始点或者基点是 Generator,这里用 $G(\_Gx ,\_Gy)$ 来表示,注意当选定一条曲线之后基点就已经确定,假如我们选定了一个很大的私钥 $\_k$,那么公钥就是 $\_k$ 个 $G$ 相加之后的结果:
Generator:
$\_Gx$ = $0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
$\_Gy$ = $0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
Private Key:
$\_k$ = 0xD45E369D8C7D3F3D8FDBE7A1DC5D00C0291D8C58B5B9C6F7A6E9B1D45D754F1B
Public Key:
$\_Kx$ = 0xBBA8D8A3F09D3F1F4E9B1D70EF3E8D3E1A2D8A4A9B704D2C3C20C3F8A0B2A7E4
$\_Ky$ = 0x4F465D8F7D8F89D7A3E6E6B191EDC5FAFA5E2A55A7D08B807B46A5C9D0A2E1A9
注意这里公钥通常是以未压缩形式或者压缩形式表示的,未压缩形式的公钥由标识符 0X04 和 $(\_Kx,\_Ky)$ 组合而成,而压缩形式的公钥由标识符 0X02 或者 0X03 和 $x$ 坐标的值以及根据 $y$ 坐标的奇偶性计算出的一个比特组成。
好了现在我们有了公钥 $K$ 和私钥 $\_k$ ,即:
$$K = \_k * G$$
现在我们来根据上面的内容来分析一下签名验签的过程:
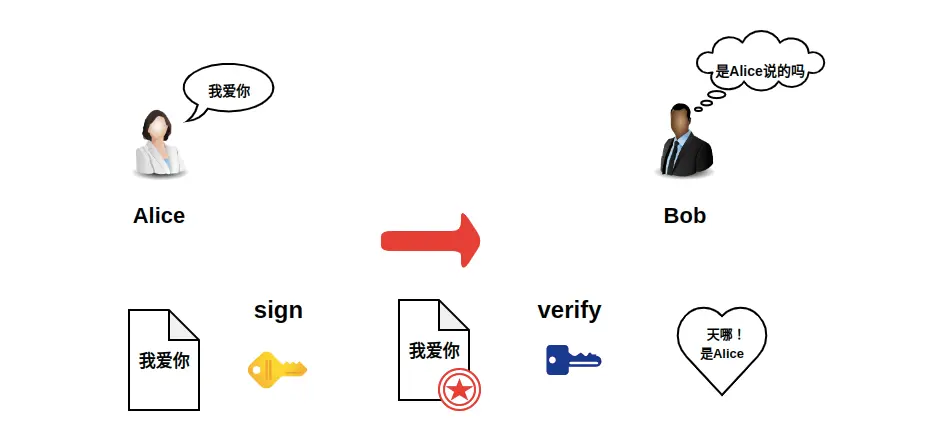
Alice 向 Bob发送消息:“我爱你”,假设这个消息为M,Alice 的私钥为 $\_k$ ,所以签名过程就是使用私钥乘以 M 的哈希值作为签名 $\_s$ :
$$\_s = \_k * hash(M)$$
现在将 M 和 $\_s$ 发送给 Bob,公钥 $K$ 在消息发送前就已经给了Bob,Bob拿到消息后先使用公钥 $K$ 与 M
的哈希值相乘得到 X ,再使用 $\_s$ 与基点 $G$ 点相乘得到 Y,如果 X == Y 则验证通过,示意图如下:
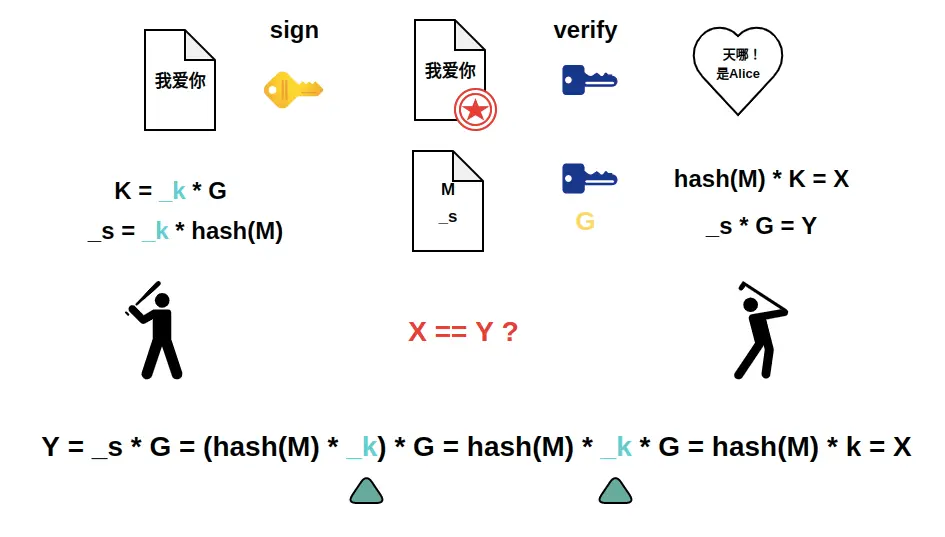
可以看到 X == Y 是成立的,同时可以明确没有私钥 $\_k$ 就无法证明,这个过程中的计算 Alice 是清楚的,但 Bob 不清楚,但他只需要验证 X == Y 成立就明确消息是Alice发出的。
但这个过程是有问题的,Bob 是可以通过 $\_s {\kern 5pt} / {\kern 5pt} hash(M) = \_k$ 得到私钥 $\_k$ 的,注意这里和上面的 $K = \_k * G$ 不一样,上面是坐标点,而这里的每个值都是数字!所以就有如下解决方案:
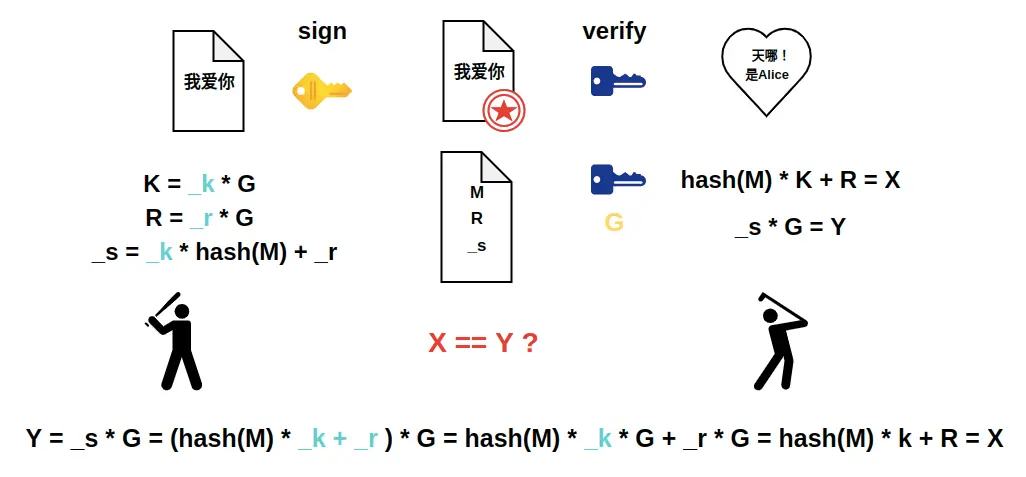
引入 R ,其存在类似公钥,这样同样可以证明 X == Y ,因此这种情况下签名文件的内容是 R 和 _s 的组合,需要注意的是这两个值是和曲线的位数有关,例如本例中 $secp256k1$ 曲线,则 R 和 _s 都是32字节,$secp192k1$ 曲线,则 R 和 _s 都是24字节,因此在不考虑ASN.1之类的存储结构,最精简的签名文件,就是单纯的 R 和 _s 的组合,以本例来说是64字节,$secp192k1$ 曲线签名文件则是48字节;
四、椭圆曲线的离散化
为什么要将椭圆曲线离散化,究其原因有如下几点:
1、椭圆曲线密码学使用的有限域是一个离散域,其中元素数量有限,所有的运算操作封闭
2、安全性:离散化可以增强椭圆曲线密码学的安全性,在椭圆曲线上。离散对数问题是一个非常困难的问题。
3、计算精度问题:在实数域上计算椭圆曲线时,会涉及到除法,比如在ECDSA签名需计算一个参数K的逆元,即 $k^{-1}$
因此需要对上面的椭圆曲线做取模运算:
$$y^{2} \equiv x^{3} + a * x + b \bmod p $$
代入本例来说即:
$$y^{2} \bmod p = (x^{3}+7) \bmod p$$
这里要说明的是 模 $p$ 需要尽可能的大,其位数由曲线位数决定,比如本例 $secp256k1$ 曲线,模 $p$ 的长度为256位。
五、参考文献
[ 1. ] SM2国密算法/椭圆曲线密码学ECC之数学原理 !
[ 2. ] 椭圆曲线演示工具
