在证明一个语言是上下文无关的时候,有两种选择:可以给出生成它的上下文无关文法,或者给出识别它的 下推自动机(PDA)。本篇所介绍的称为 下推自动机 的计算模型,很像非确定型有穷自动机,但是它有一个称为 栈 的额外设备。栈在控制器的有限存储量之外提供了附加的存储,使得下推自动机能够识别某些非正则语言。
一、对比示意图
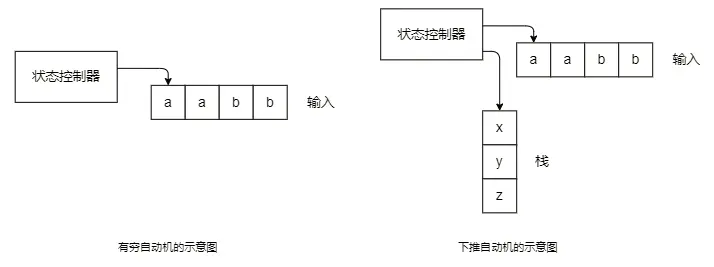
栈的作用体现在它能保存无限的信息量。有穷自动机(DFA) 不能用它的有限存储保存大数据量的字符串,所以它不能识别语言 {$0^n1^n|n \geqslant 0$},而 PDA可以用栈保存它所看见的$0$的个数,从而能识别这个语言。因此,栈的无界性使得PDA能够保存大小没有限制的数,下面的非形式化的描述关于语言 {$0^n1^n|n \geqslant 0$} 的PDA如何工作:
读取输入串的符号,每读一个$0$,把它推入栈,一旦看见$1$之后,每读一个$1$,就把一个 $0$弹出栈,当栈中的$0$被清空时恰好读完输入串,则接受这个输入。如果在还有$1$没有读的时候栈已经被清空,或者在栈中还有$0$的时候$1$已经读完了;或者$0$出现在$1$的后面,则拒绝这个输入。
二、PDA的形式化定义
$PDA \quad M=(Q,\Sigma,\delta,\Gamma ,q_0,F)$,其中
- $Q$:有穷状态集
- $\Sigma$:输入字母表,$\Sigma_{\xi} = \Sigma \cup ${$\xi$}
- $\Gamma$:栈字母表,$\Gamma_{\xi}=\Gamma \cup ${$\xi$}
- $\delta : Q \times \Sigma_{\xi} \times \Gamma_{\xi} \to P(Q \times \Gamma_{\xi})$ 转移函数
- $q_0 \in Q$:初始状态
- $ F \subseteq Q$:接受状态(终结状态)集
三、PDA计算的形式定义
- $ M=(Q,\Sigma,\delta,\Gamma ,q_0,F)$;输入 $w=w_1w_2…w_m,w_i \in \Sigma_{\xi}$
- 计算:状态–栈符号串序列
$(r_0,s_0),(r_1,s_1)…,(r_m,s_m)$,
其中 $r_i \in Q,S_i \in \Gamma^*$,满足- $(r_0,s_0)=(q_0,\xi)$
- $(r_{i+1},b) \in \delta(r_i,w_{i+1},a)$;其中$s_i=at;s_{i+1}=bt,a,b \in \Sigma_{\xi},t \in \Gamma^*$
- $r_m \in F$;(或者同时要求 $s_m=\xi$)
- $M$ 接受$w$:$M$对输入$w$存在接受计算
- $M$(识别,接受)的语言: $L(M)=${$x|M$接受$x$}
四、举例说明
假设 $L(M_1)=${$0^n1^n|n \geqslant 0$} ,$M_1=(${$q_1,q_2,q_3,q_4$},{$0,1$},{$0,\$$},$\delta,q_1,${$q_1,q_4$}$)$,则可得如下转移函数表:
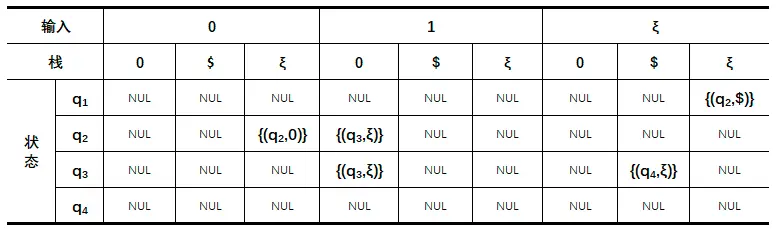
对上表略作说明:当处于 $q_1$ 状态时,可以读入空串,也不消耗栈底元素,可将 $ 压入栈底进入状态 $q_2$ ,之后读到 $0$ 压栈,读到 $1$ 将 $0$ 弹出栈,直到读到栈底元素 $ 之后结束判断是否在接受状态;
注意:
- NUL表示不允许该状态出现
- 这四种状态分别是:没有01;0比1多;0比1少;0的个数与1相同
