有穷自动机

计算理论要面对的第一个问题是：什么是计算机？现实的计算机相当复杂，很难直接为它们建立一个容易处理的数学理论，因此采用称为 计算模型 的理想计算机来描述，本篇就从最简单的 有穷自动机 讲起。

一、状态图

通常在对现实问题建立数学模型的初期，最重要的是对问题进行抽象的描述，如下图，采用状态图来描述一个有穷自动机 $M_1$：

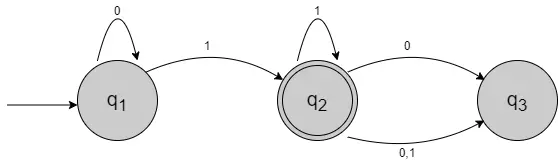
如图所示被称为 $M_1$ 的状态图，它包含3个状态，记作 $q_1$、$q_2$和$q_3$。起始状态 $q_1$ 用一个指向它的无出发点的箭头表示，接收状态 $q_2$ 带有双圈。从一个状态指向另一个状态的箭头称为转移；这里需要注意的是处理从 M₁ 的起始状态开始，自动机从左至右一个一个字符读取字符串中的所有字符，根据不同的状态转移路径到不同的状态，直到读取到最后一个字符时 $M_1$ 产生它的输出。如果 $M_1$ 现在处于接受状态，则输出为接收，否则输出为拒绝。

例如，输入的字符串为 1101 ，用上述的有穷自动机 $M_1$ 处理步骤如下：

1. 开始处于状态 $q_1$
2. 读到 1，沿着转移 $q_1$ 到 $q_2$
3. 读到 1，沿着转移 $q_2$ 到 $q_2$
4. 读到 0，沿着转移 $q_2$ 到 $q_3$
5. 读到 1，沿着转移 $q_3$ 到 $q_2$
6. 输出接受，因为在输入字符串的末端 $M_1$ 处于接受状态 $q_2$

二、有穷自动机的形式化定义

形式化定义把一台有穷自动机描述成一张含有以下5部分的表：状态集、输入字母表、动作规则、起始状态以及接受状态集。用数学语言表达，5个元素的表经常称为5元组；

这里略作解释一下 动作规则，在描述中用 转移函数 定义动作规则，常记作 $\delta$ 。如果有穷自动机从状态 $x$ 到状态 $y$ 标有输入符号 1 的箭头，这就表示它处于状态 $x$ 时读取到 1，则转移到状态 $y$，则用转移函数记作 $\delta(x,1)=y$；

因此可以描述 有穷自动机 是一个5元组 $(Q,\Sigma,\delta,q_0,F)$，其中

1. $Q$ 是一个有穷集合，称为 状态集
2. $\Sigma$ 是一个有穷集合，称为 字母表
3. $\delta: Q \times \Sigma \to Q$ 是 转移函数
4. $q_0 \in Q$ 是 起始状态
5. $F \subseteq Q$ 是 接受状态集

此时可以给出 $M_1$ 的形式化定义: $M_1 = (Q,\Sigma,\delta,q_1,F)$，其中

1. $Q =｛q_1,q_2,q_3｝$
2. $\Sigma = ｛0,1 ｝$
3. $\delta$ 描述为

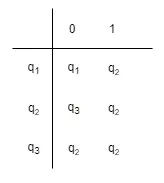
4. $q_1$是起始状态
5. $F =｛q_2｝ $

这里需要说明的是若 $A$ 是机器 $M$ 接受的全部字符串集，则称 $A$ 是机器 $M$的语言，记作$L(M)=A$。又称 **$M$识别$A$或$M$接受$A$**。一台机器可能接受若干字符串，但是永远只能识别一个语言。如果机器不接受任何字符串，那么它仍然识别一个语言，即空语言$\oslash $。

三、计算的形式化定义

设 $M = (Q,\Sigma,\delta,q_0,F)$ 是一台有穷自动机，$w=w_1w_2w_3…w_n$ 是一个字符串并且其中任一$w_i$ 是字母表 $\Sigma $ 的成员，如果存在 $Q$ 中的状态序列是 $r_0,r_1,r_2…,r_n$，满足下述条件：

1. $r_0=q_0$
2. $\delta(r_i,w_{i+1})=r_{i+1},i=0,…,n-1$
3. $r_n \in F$

则称 $M$ 接受 $w$

怎么理解呢？$r_{i+1}$ 状态都是由上一个状态 $r_i$ 以及输入的字符 $w_i$ 决定的，比如 $i = 0$ 时，$r_0 = q_0$ 即为初始状态，那么当输入为 $w_1$时，输出为 $r_1$，以此类推…，当得到 $r_n \in F$ 时，则认为 $M$ 接受 $w$。

如果 $A=｛w | M$接受$w｝$，则称 $M$ 识别语言 $A$ 。