要了解有穷自动机的能力,就必须要了解它们的局限性。我们知道能被一台有穷自动机识别的语言被称为正则语言,但在很多的时候仅凭直观的感觉往往会把我们带入歧途,这就是为什么想当然的事还需要数学证明。为此引入 泵引理 的概念
一、什么是泵引理
证明非正则性的技术源于一个关于正则语言的定理,通常称它为 泵引理 。该定理指出所有的正则语言都有一种特殊的性质。如果能证明一个语言没有这种特性,则可以保证它不是正则的。这条性质是:语言中的所有字符串只要它的长度不小于某个特定的值——泵长度,就可以被“抽取”。它的意思是指每一个这样的字符串都包括一段子串,把这段子串重复任意次,得到的字符串仍在这个语言中。
二、定理描述
若 $A$ 是一个正则语言,则存在一个数 $P$ (泵长度)使得,如果 $s$ 是 $A$ 中任一长度不小于 $P$ 的字符串,那么 $s$ 可以被分成3部分,$s=xyz$,满足以下条件:
- 对每一个 $i \geqslant 0,xy^iz \in A $
- $|y| > 0$
- $|xy| \leqslant p$
其中 $|s|$ 表示字符串 $s$ 的长度,$y^i$ 是 $i$ 个$y$ 连接在一起, $y^0$ 等于 $\xi$,$|xy|$ 表示 $xy$加在一起的长度 ;
当 $s$ 被划分成 $xyz$ 时,$x$ 和 $z$ 可以是 $\xi$ ,但是条件2说 $y \neq \xi$。可以看出如果没有条件2 ,定理显然成立,但也就没有什么意思了。
泵引理证明
设 $ A = L(M),M=(Q,\Sigma,\delta,q_1,F),s=s_1s_2s_3…s_n \in A$
令 $|Q|=p$,则有 $n \geqslant p$
设 $M$ 在$s$上计算 $r_1,r_2…r_{n+1},\delta(r_i,s_i)=r_{i+1},$
根据 鸽巢原理,存在 $j < I$,使得 $r_j = r_I,I \leqslant p+1$
令 $x = s_1…s_{j-1},y=s_j…s_{I-1},z=s_I…s_{n+1}$,此时将输入分割成三段;
由于 $x$ 让 $M$ 从$r_1$ 到 $r_j$ ,$y$ 让 $M$ 从 $r_j$ 到 $r_I$,因为 $r_j = r_I$,也可称$y$ 让 $M$ 从 $r_j$ 到 $r_j$,则 $z$让 $M$ 从 $r_j$ 到 $r_{n+1}$,而 $r_{n+1}$ 是接受状态,所以 $\forall i \geqslant 0,xy^iz \in A$;
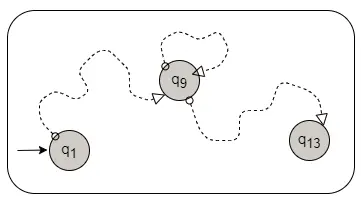
如下图给定字符串 $s$ 和 $M$ 在处理 $s$ 时经过的状态序列。状态 $q_9$ 重复出现。

现在把 $s$ 划分成三段 $x,y,z$。 $x$ 是 $s$ 在 $q_9$ 前面的部分,$y$ 是两个 $q_9$ 之间的部分,$z$ 是 $s$ 的剩余部分,即第二个 $q_9$ 以后的部分。因此, $x$ 把 $M$ 从状态 $q_1$ 带到 $q_9$,$y$ 把 $M$ 从 $q_9$ 带回到 $q_9$,$z$ 把 $M$ 从 $q_9$ 带到接受状态 $q_{13}$,如下图所示: