上述在讨论的过程中,计算的每一步都按照唯一的方式跟在前一步的后面。当机器处于给定的状态并读入下一个输入字符时,就可以唯一确定下一个状态。因此称这是 确定型计算,在 非确定型 机器中,任何一个点,下一个状态都可能存在若干个 选择。非确定型是确定型的推广,因此每一台确定型有穷自动机(简称DFA)都是一台非确定型有穷自动机(简称NFA)
一、NFA状态图
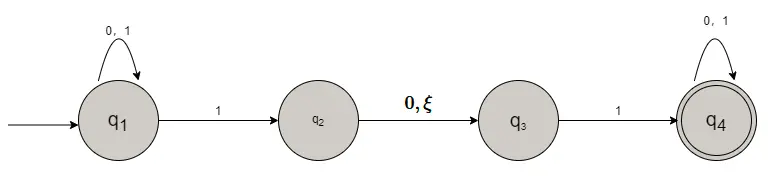
需要特别指出NFA与DFA不同之处:
- $q_1$ 对于1有两个射出的箭头;
- $q_2$ 对于1没有箭头;
- $N_1$ 中包含 $\xi $ 的箭头;
如果一个状态,在射出的箭头上标有 $\xi$ ,则不用读任何输入,机器分裂成多个备份,每一个标记 $\xi$ 的射出箭头有一个备份跟踪,还有一个备份停留在当前状态。然后机器和前面一样非确定性的运行。这里可以把非确定性看做是若干独立的“过程”或者“线程”分别的进行,如果这些子过程至少有一个接受,则整个过程计算接受。以 $N_1$ 接受 010110 的计算为例:
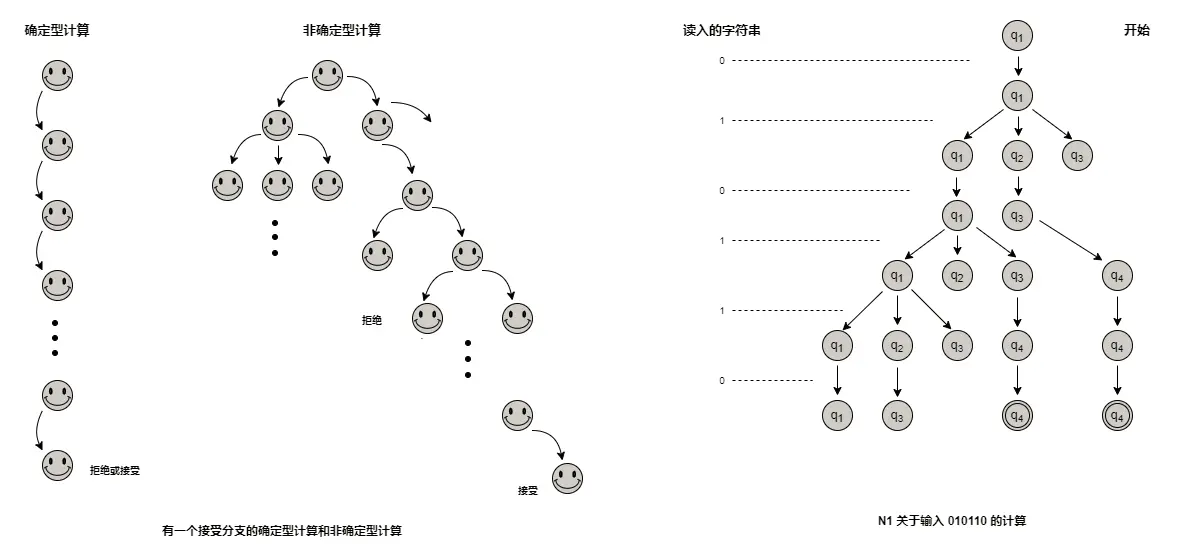
类似的给出 非确定性有穷自动机 的5元组描述 $(Q,\Sigma,\delta,q_0,F)$ ,其中
- $Q$ 是有穷的状态集
- $\Sigma$ 是有穷的字母表
- $\delta: Q \times \Sigma_\xi \to P(Q)$ 是转移函数
- $q_0 \in Q$ 是起始状态
- $F \subseteq Q$ 是接受状态集
这里的 $P(Q)$ 是任意的集合 $Q$ 的所有子集组成的集合,称 $P(Q)$ 是 $Q$ 的幂集 ;
由此我们可以用5元组来描述上面的非确定性有穷自动机:$N_1 = (Q,\Sigma,\delta,q_1,F)$,其中
- $Q={q_1,q_2,q_3,q_4} $
- $\Sigma ={0,1}$
- $\delta$ 由下表给出:
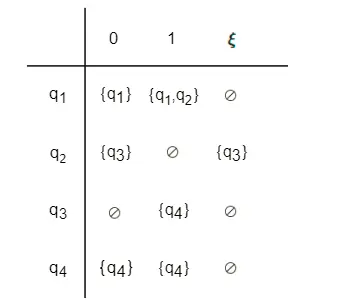
- $q_1$ 是起始状态
- $F ={q_4}$
同样 NFA 计算的形式化定义 也和 DFA 类似,设 $N = (Q,\Sigma,\delta,q_0,F)$ 是一台NFA,$w=y_1y_2y_3…y_n$ 是一个字符串并且其中任一$y_i$ 是字母表 $\Sigma $ 的成员,如果存在 $Q$ 中的状态序列是 $r_0,r_1,r_2…,r_n$,满足下述条件:
- $r_0=q_0$
- $r_{i+1} \in \delta(r_i,y_{i+1}),i=0,1,…,m-1$
- $r_m \in F$
则称 $N$ 接受 $w$;
