如果两台机器识别相同的语言,则称它们是等价的。换句话说确定型(DFA)和非确定型(NFA)有穷自动机识别相同的语言类;这个论述似乎出乎意料又是极为有用的。怎么说?出乎意料在于NFA好像比DFA能力更强,因此猜想NFA能识别更多的语言。极为有用在于给定的语言,描述识别这个语言的NFA有时比描述识别这个语言的DFA要容易的多。
一、证明定理
定理:每台NFA都有等价DFA
证明思路:
- 给定NFA,构造等价DFA
- 用DFA模拟NFA
- DFA记住NFA的所有分支
- 设NFA有 K 个状态,则共有 $2^{k}$ 个不同状态子集合
- $ \xi$ 闭包:
对每个状态子集合,经 $\xi$移动可达到的新状态子集合
具体证明如下:
设 $N = ({1,2,3},{a,b},\delta,1,{1})$,求等价的DFA
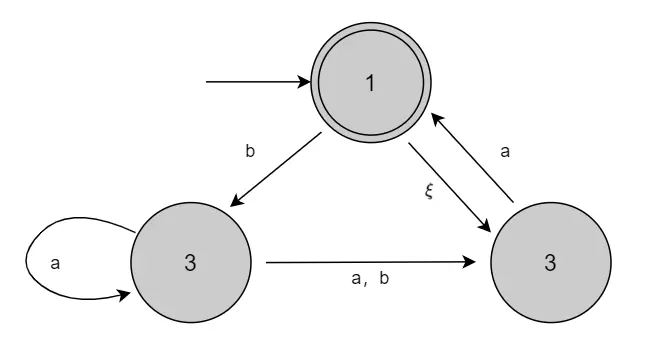
1、 写出子集状态:共有 $2^{k}$ 个不同状态子集合
分别为:$\oslash,{1},{2},{1,2},{3},{1,3},{2,3},{1,2,3} $
2、求 $\xi$ 闭包
$E({1}={1,2,3})$
3、 添加转移
4、接受状态
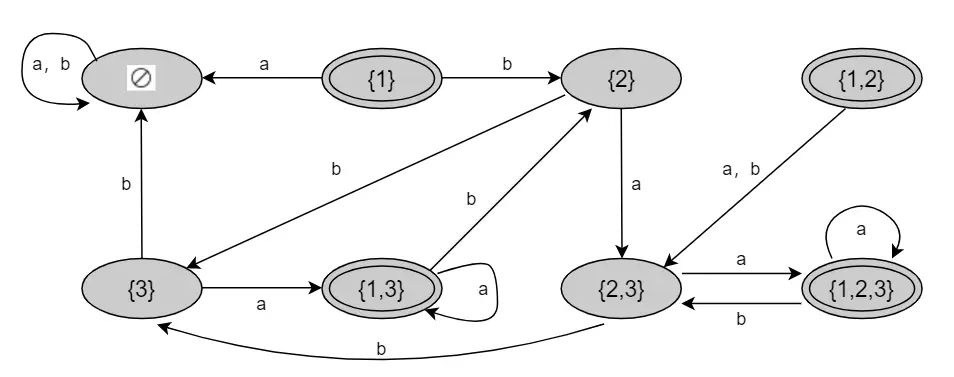
5、删除不可达状态
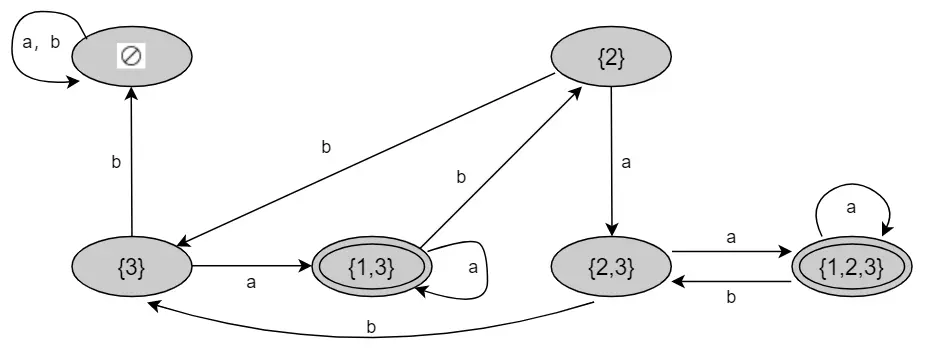
注意这里的 不可达状态 指的是没有箭头指向的状态,意味着没有任何情况可以到达这个状态;
根据上图可写出 DFA 的5元组,至此就完成了 NFA 到 DFA 的转换
