CRC校验的数学原理及算法实现

2024-10-10

4022 字

一、基本概念

为了更好的描述以及理解 CRC 校验 (循环冗余校验码)的原理，这里先来对一些概念进行描述。CRC是基于有限域GF(2)(即除以2的同余)的多项式环，那现在引申出两个问题：

1.1 什么是有限域？

有限域，也叫做伽罗瓦域（Galois field），是数学中一种特殊的代数结构。通俗地讲，有限域就是一个有穷个元素的集合，在这个集合里可以进行加法和乘法运算，并且这些运算满足一些特定的规则。

最常见的有限域莫过于模素数 $p$ 有限域 $GF(p)$

$GF(p)$ 是定义在证书集合 $\{0,1,2….,p-1\}$ 上的域，它的具备的基本运算时和我们常规理解的有些类似但却不同，例如 $GF(7)$ 定义在 $\{0,1,2,3,4,5,6\}$ 上的一个有限域，下面我们来演示一下相应的基本运算：

1.1.1 模加法

模加法类似于普通的加法运算，唯一不同的是，当运算的结果超出范围时，要将运算结果对素数 $p$ 取模：

$$1 + 2 = 3 {\kern 5pt} mod {\kern 5pt} 7 = 3 \\ 5 + 6 = 11 {\kern 5pt} mod {\kern 5pt} 7 = 4 $$

1.1.2 模乘法

同样类似于普通的乘法运算，超出范围时取模

$$1 \ast 2 = 2 {\kern 5pt} mod {\kern 5pt} 7 = 2 \\ 4 \ast 5 = 20 {\kern 5pt} mod {\kern 5pt} 7 = 6$$

1.1.3 模减法

$a$ 减去 $b$ ,其实就是 $a$ 加上 $b$ 的加法逆元，关键是找到 $b$ 的加法逆元，所谓加法逆元我们可以通过如下过程来了解：

在 $GF(7)$ 中，每个非零元素都有一个唯一的相反数，即：

1 的相反数是 6，因为 1 + 6 = 7 ≡ 0 mod 7
2 的相反数是 5，因为 2 + 5 = 7 ≡ 0 mod 7
3 的相反数是 4，因为 3 + 4 = 7 ≡ 0 mod 7
4 的相反数是 3，因为 4 + 3 = 7 ≡ 0 mod 7
5 的相反数是 2，因为 5 + 2 = 7 ≡ 0 mod 7
6 的相反数是 1，因为 6 + 1 = 7 ≡ 0 mod 7

这里所说的 相反数 就是加法逆元。因此当我们在计算 3-1 时，其运算过程如下：

$$3 - 1 = 3 + (-1) = 3 + 6 = 9 {\kern 5pt} mod {\kern 5pt} 7 = 3$$

总结来说，在有限域中进行减法运算，可以转化为加上另一个元素的相反数，并最终取模。这样可以确保结果仍然在有限域内。

1.1.4 模除法
$a$ 除以 $b$，需要找到 $b$ 的乘法逆元,即满足以下式子的整数 $x$：

$$bx = 1 {\kern 5pt}mod {\kern 5pt} 7$$

也就是解如下方程：

$$bx =1+7k，其中k∈Z^{+}$$

关于此函数的求解方式此处不再赘述，仅以示例略作说明：

$$3 {\div} 4 = 3 * (4^{-1}) = 3 * 2 = 6 {\kern 5pt}mod {\kern 5pt}7 = 6$$

综上所述，有限域就像是在一个封闭的系统内进行数学运算，尽管看起来这个运算法则和我们日常生活中使用的不尽相同。

1.2 什么是多项式环？

一个多项式是由一系列项组成的，每一项都是一个系数乘以未知数的幂次。例如：

$$P(x) = 3x^{2} + 2x + 1$$

这里的每一项都是一个系数 $(3、2、1)$乘以 $x$ 的不同幂次 $(x^{2}、x、1)$ 这些系数可以是任何数字，比如整数、分数或者是其他更复杂的数。所谓 多项式环 ，其实是一个数学结构，它包括了所有可能的多项式，并且在这个结构内进行相关的基本运算。

例如存在两个多项式 $P(x)$ 和 $Q(x)$ ，在做加法运算时，可以将对应项的系数相加，得到一个全新的多项式：

$$P(x) = 3x^{2} +2x + 1 \\ Q(x) = 2x^{2}+4x+3 \\ P(x) + Q(x) = (3x^{2} +2x + 1) + (2x^{2}+4x+3) = 5x^{2}+6x+4$$

其他类型运算也大致类似，最常见的多项式环是整系数多项式环 $Z[x]$，它包含了所有系数为整数的多项式。在这个环中，可以进行各种基本运算，并且结果仍然是一个整系数多项式。

1.3 CRC基础概念

在文章开头，给出了 CRC 校验所使用的基础数学概念：CRC是基于有限域 $GF(2)$ (即除以2的同余)的 多项式环。这句话怎么理解呢？简单来说，就是 所有系数都为 0 或 1 (又叫做二进制) 的多项式集合，并且集合对于所有的代数操作都是封闭的。例如：

$$(x^{2} + x) +(x +1) = x^{3}+2x+1 ≡ x^{3}+1$$

$2x$ 这一项之所以消失，是因为对系数的加法运算会取 2 的模数，这导致这一项的系数为 0 。类似的乘法也是如此：

$$(x^{2} +x)(x + 1) = x^{3}+2x^{2}+x≡x^{3}+x$$

现在我们试着多项式做除法：

$$\frac{x^{3}+x^{2}+x}{x+1} = (x^{2}+1) - \frac{1}{(x+1)}$$

也就是说：

$$(x^{3}+x^{2}+x) = (x^{2}+1)(x+1)-1$$

这等价于：

$$(x^{2}+x^{1}+1)x = (x^{2}+1)(x+1)-1$$

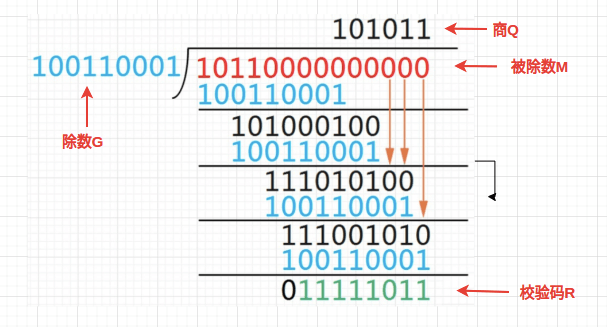
这里除法得到了商 $x^{2} + 1$ 和余数 -1 。字符串中每一位其实就对应了这样类型的多项式的系数。为了得到 CRC，首先将其乘以 $x^{n}$ ,这里 $n$ 是一个固定多项式的阶数，然后再将其除以这个固定的多项式，余数的系统就是 CRC 。

在上面的等式中，$x^{2}+x^{1}+1$ 表示了本来的信息位是 111 ，$x+1$ 就是所谓的钥匙，而余数是 1 ($x^{0}$) 就是 CRC , key 的最高次为 1 , 所以将原来的信息乘以 $x^{1}$ 得到 $x^{3}+x^{2}+x$ , 也可以视为原来的信息位补 1 个零成为 1110 。

现在我们根据上面的等式来定义一般式：

$$M(x) \cdot x^{n} = Q(x) \cdot G(x) - R(x)$$

这里 $M(x)$ 是原始的信息多项式， $G(x)$ 是 $n$ 阶的 “钥匙” 多项式。$M(x) \cdot x^{n}$ 表示了将原始信息后面加上 $n$ 个 0 。$R(x)$ 是余数多项式，即是 CRC校验和。在通信中，发送者在原始的信息数据 $M$ 后面附加上 $n$ 位的 $R$ 之后发送接受者收到 $M$ 和 $R$ 后，检查 $M(x) \cdot x^{n} + R(x)$ 是否能被 $G(x)$ 整除，如果是则认为该信息正确，否在就认为该信息存在错误。说的更直白些 CRC的本质是除法，把待检验的数据当作一个很大（很长）的被除数，两边选定一个除数（有的文献叫poly），最后得到的余数就是CRC的校验值。

1.4 生成多项式

在 1.3 中提到的 $G(x)$ 就是现在我们所说的生成多项式，由算法的定义和实际工程的要求，我们可以得出生成多项式的特性。

1.4.1 特性要求

不可约性

理想的CRC多项式应当是不可约的，即不能分解为两个非平凡多项式的乘积。不可约多项式有助于确保CRC的检错能力更强

奇偶性

某些CRC多项式具有类似素数的特性，即除了1和自身外没有其他因数。这种多项式可以增加CRC检测突发错误的能力

最小距离

CRC多项式应当能够区分不同的错误模式。理想情况下，不同的错误模式应当产生不同的CRC值。最小距离是指两个不同的错误模式所产生的CRC值之间的最小差异。较大的最小距离意味着更高的检错能力

检测特定错误模式的能力

理想的CRC多项式应当能够检测以下几种错误模式：

单比特错误：一个位错误。
双比特错误：两个位错误。
短突发错误：连续多个位错误。
长突发错误：某些情况下，长的连续错误也能被检测出来

易于硬件实现

CRC多项式的设计应当考虑到硬件实现的简便性和效率。例如，某些多项式在硬件实现中更为简单

1.4.2 多项式参数模型

同样的 CRC 多项式，调用不同的 CRC 计算函数，得到的结果却不一样，而且和手算的结果也不一样，这就涉及到 CRC 的参数模型了。计算一个正确的 CRC 值，需要知道 CRC 的参数模型，一个完整的CRC参数模型应该包含以下信息：WIDTH、POLY、INIT、REFIN、REFOUT、XOROUT等：

WIDTH ：宽度，即生成的CRC数据位宽，如CRC-8，生成的CRC为8位
POLY：十六进制多项式，省略最高位1，如 $x^8 + x^2 + x + 1$，二进制为1 0000 0111，省略最高位1，转换为十六进制为 0x07
INIT： CRC初始值，和WIDTH位宽一致。
XOROUT：计算结果与此参数进行异或运算后得到最终的 CRC 值，和 WIDTH 位宽一致。
REFIN：输入是否反转，true 或 false，在进行计算之前，原始数据是否翻转，如原始数据：0x34 = 0011 0100，如果REFIN为 true，进行翻转之后为0010 1100 = 0x2c
REFOUT：输出是否反转，true 或 false，运算完成之后，得到的CRC值是否进行翻转，如计算得到的CRC值：0x97 = 1001 0111，如果REFOUT为 true，进行翻转之后为 11101001 = 0xE9。

通常如果只给了一个多项式，其他的没有说明则：INIT=0x00，REFIN= false，REFOUT= false，XOROUT=0x00。

常用的一些 CRC 参数模型如下：

CRC算法名称	多项式公式	宽	多项式	初始值	结果异或	输入反转	输出反转
CRC-4/ITU	$x^4 + x + 1$	4	03	00	00	true	true
CRC-5/EPC	$x^5 + x^3 + 1$	5	09	09	00	false	false
CRC-5/ITU	$x^5 + x^4 + x^2 + 1$	5	15	00	00	true	true
CRC-5/USB	$x^5 + x^2 + 1$	5	05	1F	1F	true	true
CRC-6/ITU	$x^6 + x + 1$	6	03	00	00	true	true
CRC-7/MMC	$x^7 + x^3 + 1$	7	09	00	00	false	false
CRC-8	$x^8 + x^2 + x + 1$	8	07	00	00	false	false
CRC-8/ITU	$x^8 + x^2 + x + 1$	8	07	00	55	false	false
CRC-8/ROHC	$x^8 + x^2 + x + 1$	8	07	FF	00	true	true
CRC-8/MAXIM	$x^8 + x^5 + x^4 + 1$	8	31	00	00	true	true
CRC-16/IBM	$x^{16} + x^{15} + x^2 + 1$	16	8005	0000	0000	true	true
CRC-16/MAXIM	$x^{16} + x^{15} + x^2 + 1$	16	8005	0000	FFFF	true	true
CRC-16/USB	$x^{16} + x^{15} + x^2 + 1$	16	8005	FFFF	FFFF	true	true
CRC-16/MODBUS	$x^{16} + x^{15} + x^2 + 1$	16	8005	FFFF	0000	true	true
CRC-16/CCITT	$x^{16} + x^{12} + x^5 + 1$	16	1021	0000	0000	true	true
CRC-16/CCITT-FALSE	$x^{16} + x^{12} + x^5 + 1$	16	1021	FFFF	0000	false	false
CRC-16/X25	$x^{16} + x^{12} + x^5 + 1$	16	1021	FFFF	FFFF	true	true
CRC-16/XMODEM	$x^{16} + x^{12} + x^5 + 1$	16	1021	0000	0000	false	false
CRC-16/DNP	$x^{16} + x^{13} + x^{12} + x^{11} + x^{10} + x^8 + x^6 + x^5 + x^2 + 1$	16	3D65	0000	FFFF	true	true
CRC-32	$x^{32} + x^{26} + x^{23} + x^{22} + x^{16} + x^{12} + x^{11} + x^{10} + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1$	32	04C11DB7	FFFFFFFF	FFFFFFFF	true	true
CRC-32/MPEG-2	$x^{32} + x^{26} + x^{23} + x^{22} + x^{16} + x^{12} + x^{11} + x^{10} + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1$	32	04C11DB7	FFFFFFFF	00000000	false	false

二、CRC计算

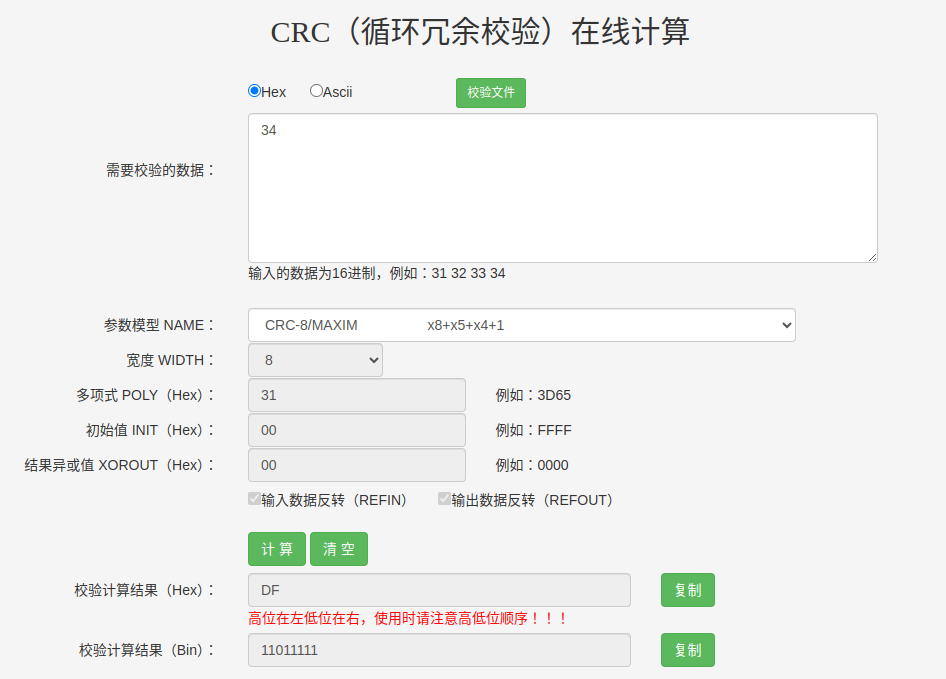
这里我们选取 CRC-8/MAXIM 这个参数模型，假如我要传递的原始数据为 ‘4’，其十六进制为 0x34 , 二进制表示方式为 110100，现在可以得到如下信息：

POLY = 0x31 = 0011 0001(最高位1已经省略)
INIT = 0x00
XOROUT = 0x00
REFIN = TRUE
REFOUT = TRUE

2.1 正向计算

正向计算是指完全按照 CRC 原理实现校验：

开始计算：

0.原始数据 = 0x34 = 0011 0100，多项式 = 0x31 = 1 0011 0001
1.INIT = 00，原始数据高8位和初始值进行异或运算保持不变。
2.REFIN为TRUE，需要先对原始数据进行翻转：0011 0100 > 0010 1100
3.原始数据左移8位，即后面补8个0：0010 1100 0000 0000
4.把处理之后的数据和多项式进行模2除法，求得余数：
原始数据：0010 1100 0000 0000 = 10 1100 0000 0000
多项式：1 0011 0001
模2除法取余数低8位：1111 1011
5.与XOROUT进行异或，1111 1011 xor 0000 0000 = 1111 1011 
6.因为REFOUT为TRUE，对结果进行翻转得到最终的CRC-8值：1101 1111 = 0xDF

C语言描述如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>


#define INIT_VALUE 0
#define POLY 0x31
#define XOR 0

unsigned char reverse8(unsigned char data)
{
    unsigned char i;
    unsigned char temp = 0;
    for (i = 0; i < 8; i++) // 字节反转
        temp |= ((data >> i) & 0x01) << (7 - i);
    return temp;
}

unsigned char crc8_maxim(unsigned char *addr, int num)
{
    unsigned char data;
    unsigned char crc = INIT_VALUE; // 初始值
    int i;
    for (; num > 0; num--)
    {
        data = *addr++;
        data = reverse8(data); // 字节反转

        crc = crc ^ data;       // 与crc初始值异或
        for (i = 0; i < 8; i++) // 循环8位
        {
            if (crc & 0x80) // 左移移出的位为1，左移后与多项式异或
            {
                crc = (crc << 1) ^ POLY;
            }
            else // 否则直接左移
            {
                crc <<= 1;
            }
        }
    }
    crc = reverse8(crc);
    crc = crc ^ XOR ; // 最后返与结果异或值异或
    return (crc);          // 返回最终校验值
}

int main(void)
{
    unsigned char buff[1] = {0x34};
    printf("crc=%hhx\n", crc8_maxim(buff, 1));
    return 0;
}

可以看到在上述实现方式中会存在逐字节反转的行为，这会耗费更多的时间，存在效率问题，因此引出 反向计算 的方式。

2.2 反向计算

一般来说输入和输出反转都是同时的，输入输出的反转就是把式子做镜像翻转，但是反转计算直接右移即可，不用考虑移出去的数据还会有影响，如下图所示：

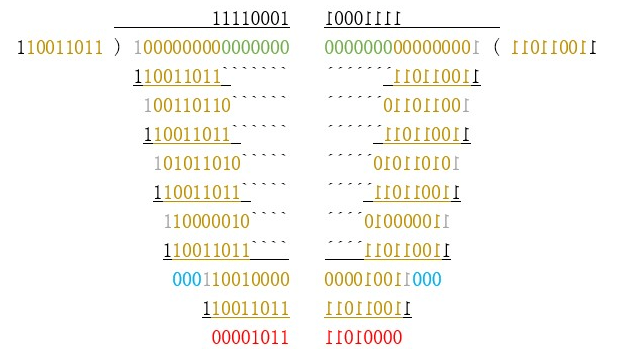
左侧为正向计算，右侧为反向计算。C代码实现为：

unsigned char crc8_maxim(unsigned char *data, int length)
{
    unsigned char i;
    unsigned char crc = 0; // Initial value
    while (length--)
    {
        crc ^= *data++; // crc ^= *data; data++;
        for (i = 0; i < 8; i++)
        {
            if (crc & 1)
            {
                crc = (crc >> 1) ^ 0x8C; // 0x8C = reverse 0x31
            }      
            else{
                crc >>= 1;
            }  
        }
    }
    return crc;
}

int main(void)
{
    unsigned char buff[1] = {0x34};
    printf("crc=%hhx\n", crc8_maxim(buff, 1));
    return 0;
}

更多算法见 CRC原理计算

2.3 查表法

为了便于理解查表法，我将 2.2 章节中部分代码摘录如下：

for (i = 0; i < 8; i++)
{
    if (crc & 1)
    {
        crc = (crc >> 1) ^ 0x8C;
    }      
    else{
        crc >>= 1;
    }  
}

观察上面代码，仔细这个 for 循环可以生成一个表。进入for循环的变量 crc 大小为1个字节，即变量 crc 的大小可以为 0-255 之间的任何一个值，并且也只能是 0-255 之间的一个值。因此，可以实现将 0-255 都经过这个 for 循环，生成对应的值，生成的值也是 0-255，这些生成的值就是crc要查的表，而传入for循环的变量 crc 就是表的索引值：


#include <stdint.h>
#include <stdio.h>

// CRC-8/MAXIM 生成多项式
#define POLY_MAXIM 0x31

// 初始化 CRC-8/MAXIM 查找表
static uint8_t crc8_table[256];

void generate_crc8_table(void)
{
    uint16_t i, j;
    for (i = 0; i < 256; ++i)
    {
        uint8_t crc = i;
        for (j = 8; j; --j)
        {
            if (crc & 1)
                crc = (crc >> 1) ^ 0x8C;
            else
                crc = crc >> 1;
            crc &= 0xFF; // 确保只保留8位
        }
        crc8_table[i] = crc;
    }
}

uint8_t crc8_maxim(const unsigned char *data, size_t len)
{
    uint8_t crc = 0;
    while (len--)
    {
        crc = crc8_table[(crc ^ *data++) & 0xFF];
    }
    return crc;
}

int main()
{
    const unsigned char data[] = {0x34};
    size_t len = sizeof(data);
    generate_crc8_table(); // 生成查找表
    uint8_t crc = crc8_maxim(data, len);
    printf("CRC-8/MAXIM of '0x34' is: 0x%02X\n", crc);
    return 0;
}

查表法其实就是以空间换效率，更多算法见 CRC查表法

2.4 验证

此时我们可以通过在线的 CRC校验工具，来验证：

Theme Preview

文章目录

分类

标签

归档

最新文章