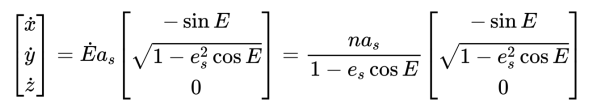一、理论基础
在高精度定位系统中,仅靠经典牛顿力学是不够精准的,在实际建模中必须引入更复杂的修正方法来补偿真实轨道中受到的多种扰动影响,比如 :
- 地球非球形引力场
- 月球、太阳等对卫星的引力影响
- 太阳辐射压力、大气阻力、潮汐效应等
- 广义相对论的引力时间膨胀效应
- 狭义相对论的运动时间膨胀效应
因此可以说牛顿万有引力是 GPS 轨道建模的 起点和基础,但为了达到所需的高精度,必须结合相对论修正和复杂的摄动模型。这也是现代航天动力学的标准做法:理论 + 观测 + 修正 = 高精度轨道。
二、开普勒轨道参数
假设地球和卫星都是理想的球体,并且卫星仅仅受到地球引力的作用,这种理想状态下的卫星运动轨道就称为 无摄运动轨道 ,它可以使用开普勒三大行星运行定律来描述,这也是本章的主要内容。
2.1 开普勒定律
- 第一定律(轨道定律):行星绕太阳沿椭圆轨道运动,太阳位于一个焦点。
- 第二定律(面积定律):单位时间扫过的面积相等(角动量守恒)。
- 第三定律(周期定律):轨道周期的平方与半长轴的立方成正比。
2.2 GPS卫星运行轨道
GPS 接收机并不是直接从牛顿万有引力定律出发来计算卫星的空间位置。实际上,GPS 的地面监控部分通过持续的接收、测定卫星发射的信号来确定卫星的运行轨道,然后推算出一组以时间为函数的轨道参数来精确描述、预测卫星的运行轨道,再将这些轨道参数上传给卫星,并让卫星转播。GPS 接收机正是从卫星信号上获取这些参数,然后根据这些参数计算出卫星的位置和速度。
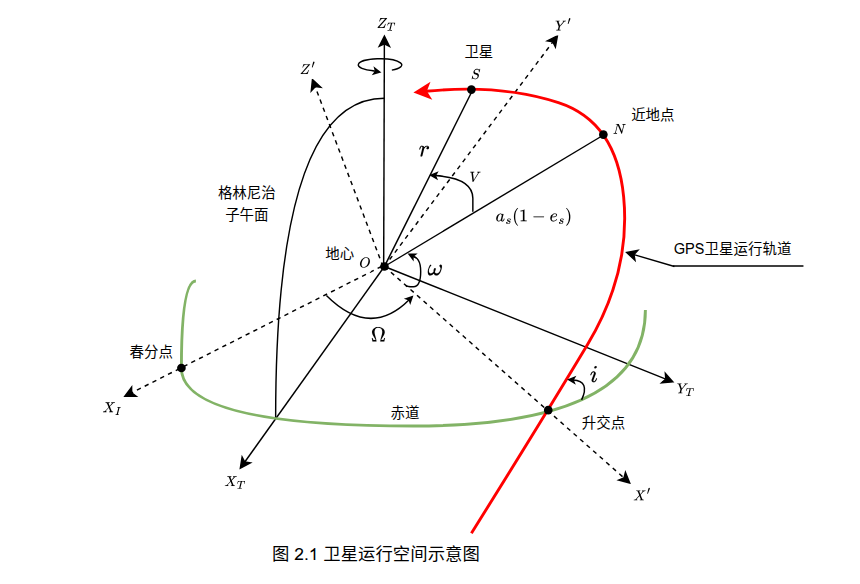
GPS 卫星的无摄椭圆轨道运动可以用一套应用广泛的开普勒轨道参数描述或者称为开普勒根数,参数共包括6个:
- 轨道升交点赤经 $\Omega$ : 赤道平面上的春分点和升交点对地心$O$的夹角,来确定卫星轨道升交点在赤道平面内的方位
- 轨道倾角 $i$ : 卫星轨道平面与赤道面的夹角,来确定卫星轨道平面相对于地心的方位
- 近地点角距 $\omega$ : 卫星轨道平面上的升交点与近地点N的地心夹角,来确定椭圆轨道的长轴和短轴的位置
- 长半径 $a_{s}$ : 椭圆轨道长半轴的大小
- 偏心率 $e_{s}$ : 椭圆轨道偏心率,与长半径 $a_{s}$ 一起确定椭圆轨道的大小和形状
- 真近点角 $v$ : 卫星在运行轨道上的当前位置 $S$ 与近地点 $N$ 的地心夹角,即 $\angle NOS$
可以看出除了真近点角$v$之前其他的5个参数都是常数和时间无关,但是真近点角$v$与时间函数关系比较复杂,因此常常使用 偏近点角$E$ 和 平近点角$M$ 来代替,借助这两个辅助量来推算真近点角$v$ 。
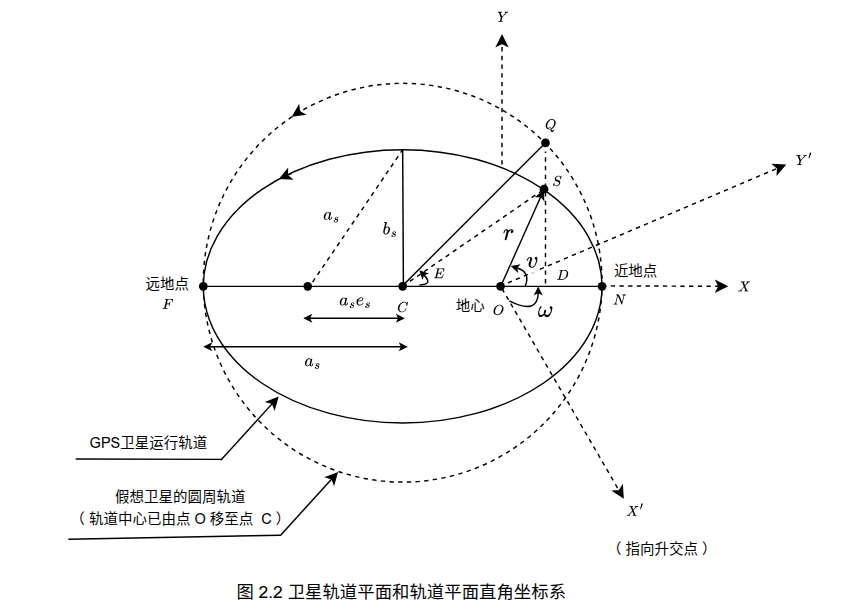
图 2.2 对应图 2.1 中的卫星轨道平面,其中在 $t$ 时刻真实卫星的 平近点角$M$ 定义为假想卫星的运行角距,即
$$M = n(t-t_{0})$$
偏近点角$E$ 和 平近点角$M$ 之间的关系由开普勒方程给出:
$$M = E -e_{s}\sin E$$
这样借助于与时间成简单线性关系的平近点角 $M$ 与几何关系确定卫星瞬时位置的真近点角 $v$ , 不过在这里之前有必要先来了解一下 开普勒方程 。
2.3 开普勒方程
如图2.2所示,其中辅助圆的扇形面积 $A_{NCQ}$ 可表示如下:
$$A_{NCQ} = \frac{E}{2\pi} \cdot \pi a^2 = \frac{1}{2} a^{2}E$$
根据椭圆与圆的 仿射变换 原则,可以得到如下性质:
椭圆是圆经过仿射变换(非均匀缩放)得到的图形,其面积的变化等于两个主方向缩放因子的乘积。
这样辅助圆上的点 $Q$ 的坐标可以表示为 $(a\cos E,a\sin E)$, 椭圆轨道上的点 $S$ 就可以表示为 $(a\cos E,b\sin E)$ 。那么椭圆扇形面积 $A_{NCS}$ 可以表示为:
$$A_{NCS} = \frac{b}{a} \cdot A_{NCQ} = \frac{1}{2} abE$$
然而,开普勒第二定律描述的是相对于焦点 $O$的面积速度,而不是椭圆中心。因此需要减去由于焦点偏移导致的三角形面积 $A_{\bigtriangleup OCS}$ :
$$A_{\bigtriangleup OCS} = \frac{1}{2} \cdot L_{OC} \cdot H_{SD} = \frac{1}{2} \cdot (ae) \cdot (b\sin E)$$
因此卫星实际扫过的面积(相较于地心$O$)为:
$$A_{NOS} = A_{NCS} - A_{OCS} = \frac{1}{2} abE - \frac{1}{2} abe \sin E = \frac{1}{2} ab(E - e\sin E)$$
同时根据开普勒第二定律(面积定律),天体在椭圆轨道上单位时间扫过的面积相等,即面积与时间成正比,则:
$$\frac{A(t)}{总面积} = \frac{t-t_{0}}{T} \Rightarrow A(t) = \frac{\pi ab}{T} (t-t_{0})$$
而 $n = \frac{2\pi}{T}$ , 所以 $\frac{\pi}{T} = \frac{n}{2}$ , 代入得 :
$$A(t) = ab \cdot \frac{n}{2}(t - t_{0})$$
两式相等:
$$\frac{ab}{2}(E-e\sin E) = ab \cdot \frac{n}{2}(t-t_{0}) \Rightarrow E - e\sin E = n(t - t_{0})$$
根据定义有 $M = n(t-t_{0})$ ,则可得到上述所说的开普勒方程:
$$M = E -e_{s}\sin E$$
注意开普勒方程属于超越方程,没有严格的分析解法(已知$M$求$E$),但 $M$ 是随时间而变化的一个值,所以当给定一个 $M$ 值后,就可以采用简单迭代方法,将 $E$ 解算出来,可以将上式改为一下的迭代形式:
$$E_{n} = M + e_{s}\sin (E_{n-1})$$
式中,$n$ 为迭代次数,在第一次的迭代中,$E$ 的初值 $E_{0}$ 可赋值为 $M$ , 直到满足精度要求即可。
2.4 真近点角推导
椭圆轨道上任意一点可以用偏近点角$E$表示为:$(a\cos E,b\sin E)$ ,其中 $b = a\sqrt{1-e^{2}}$ 是半短轴。所以可以得到当前卫星的坐标:
$$S_{卫星} = (a\cos E,a\sqrt{1-e^{2}}\sin E)$$
显然椭圆轨道的焦点$O$的坐标为 $F = (ae,0)$,向量 $\overrightarrow{OS}$ 表示为:
$$\overrightarrow{OS} = (x-ae,y)=(a\cos E -ae,a\sqrt{1-e^{2}}\sin E) = a(\cos E -e,\sqrt{1-e^2}\sin E)$$
计算距离 $r = \left | \overrightarrow{OS} \right |$ :
$$r = \left | \overrightarrow{OS} \right | = a\sqrt{(\cos E -e)^{2} + (1-e^{2})\sin^{2} E} \\ = a(1-e\cos E)$$
真近点角$v$ 是向量 $\overrightarrow{OS}$ 与长轴的夹角,所以有:
$$\cos v = \frac{L_{OD}}{L_{OS}} = \frac{x-ae}{r} = \frac{a\cos E -ae}{a(1-e\cos E)} = \frac{\cos E -e}{1-e\cos E}$$
$$\sin v = \frac{L_{SD}}{L_{OS}} = \frac{y}{r} = \frac{a\sqrt{1-e^{2}}\sin E}{a(1-e\cos E)} = \frac{\sqrt{1-e^{2}}\sin E}{1-e\cos E}$$
所以现在我们可以得到真近点角$v$ :
$$v = arctan(\frac{\sqrt{1-e^{2}}\sin E}{\cos E - e})$$
现在可以用 $(r,v)$ 来表示卫星所在位置的极坐标,转换为图2.1中所示的轨道平面直角坐标系 $(X,Y)$ 中的坐标,即
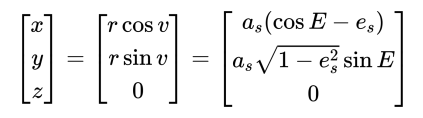
将上式对时间求导,可以得到卫星在轨道平面直接坐标系 $(X,Y)$ 中的运行速度: