一、坐标系转换公式
1.1 旋转变换
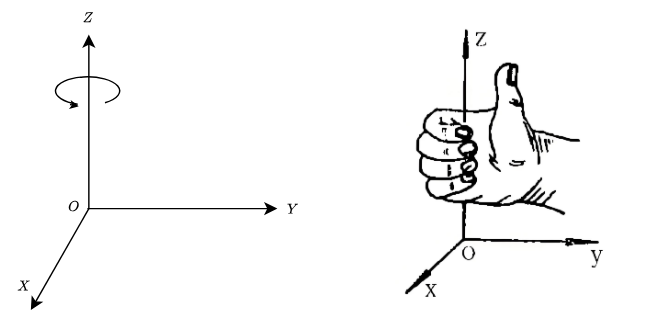
在旋转变换前,需要先规定角度的方向。右手坐标系中角度遵循右手法则,即:右手大拇指朝向坐标轴正向,其余四指方向为旋转正方向,后面所说的角度都遵循这个标准:
假设有点 $P(x,y,z)$ 经坐标变换之后得到点 $P_{1}(x_{1},y_{1},z_{1})$ ,点 $P$ 到原点的距离为 $r$ ,与相应轴的夹角为 $\varphi$ , 在新坐标系中,由于坐标系逆时针旋转了 $\theta$ , 则点 $P$ 相对于相应轴的角度变为 $\varphi - \theta$
- 绕 $Z$ 轴逆时针旋转 $\theta$
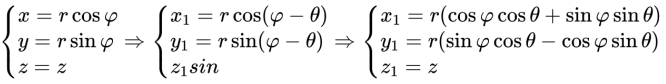
代入 $x = r\cos \varphi$ 和 $y = r \sin \varphi$ :
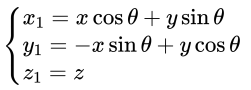
改为矩阵形式:
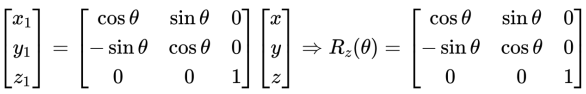
- 绕 $X$ 轴逆时针旋转 $\theta$
同理可推得:
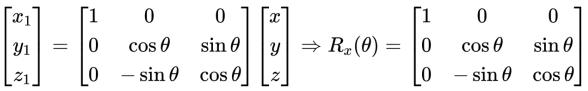
- 绕 $Y$ 轴逆时针旋转 $\theta$
同理可推得:
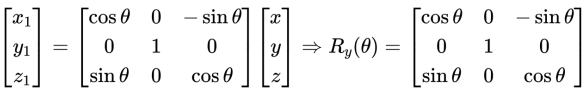
注意这是 坐标系旋转 (点不动,坐标轴旋转),这并不是点的旋转。若是 点绕原点逆时针旋转 ,则旋转矩阵与上述矩阵互为转置 ,即逆变换。
1.2 平移变换
坐标系平移是指将坐标系中的所有点沿指定方向移动固定距离的变换,保持坐标轴方向不变。如下所示:
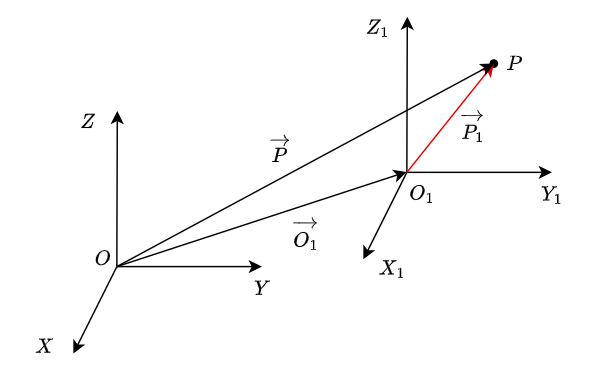
坐标系从原点 $O$ 平移到 $O_{1}$ ,但空间中点 $P$ 位置保持不变,假设:
- $\vec{P} = (x,y,z)$ , 表示点 $P$ 在原坐标系中的位置向量
- $\vec{O_{1}} = (a,b,c)$ ,表示新原点 $O_{1}$ 在原坐标系中的位置向量
- $\vec{P_{1}} = (x_{1},y_{1},z_{1})$ ,表示点 $P$ 在新坐标系中的位置向量
则存在这样关系:
$$\vec{P_{1}} = \vec{P} - \vec{O_{1}}$$
为了可以将平移操作表示为矩阵乘法,便于旋转、缩放等变换组合,可将三维坐标系平移的公式改为齐次坐标形式:
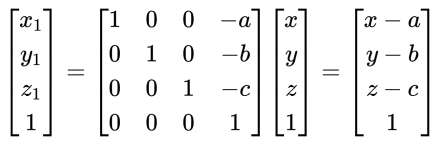
齐次坐标中点 $P$ 使用4维向量$[x_{1},y_{1},z_{1},1]^{T}$ 表示,同时平移是通过矩阵乘法实现的,不再是加法 , 可以表现为如下矩阵的乘法,其中$T$ 为平移矩阵:
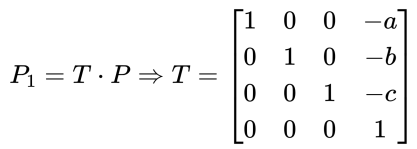
1.3 组合变换
假如同时存在旋转和平移,其中 $P(x,y,z)$ 表示变换前的坐标,$P_{1}(x_{1},y_{1},z_{1})$ 表示变换后的坐标,$R$ 为 1.1 中的旋转矩阵,$\vec{t}=(t_{x},t_{y},t_{z})$ 表示平移向量,按照缩放、旋转、平移的顺序,则有:
$$\vec{P_{1}} = R \cdot \vec{p} + \vec{t}$$
这个公式中包含 矩阵乘法 + 向量加法 ,不方便组合,因此改为齐次坐标形式:
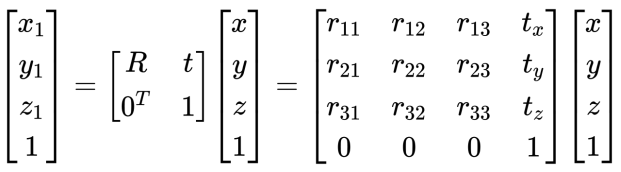
其中 $0^{T}$ 是为了保证齐次坐标的正确性和变换的放射性,最后一行经过计算之后保证了齐次坐标的第4个分量仍然是 1 ,表示它仍然是个点,而不是方向向量或者无穷远点。
二、WGS84坐标系的转换
在 卫星的无摄运动轨道分析 一文中,详细描述了卫星运动轨迹及相关参数:
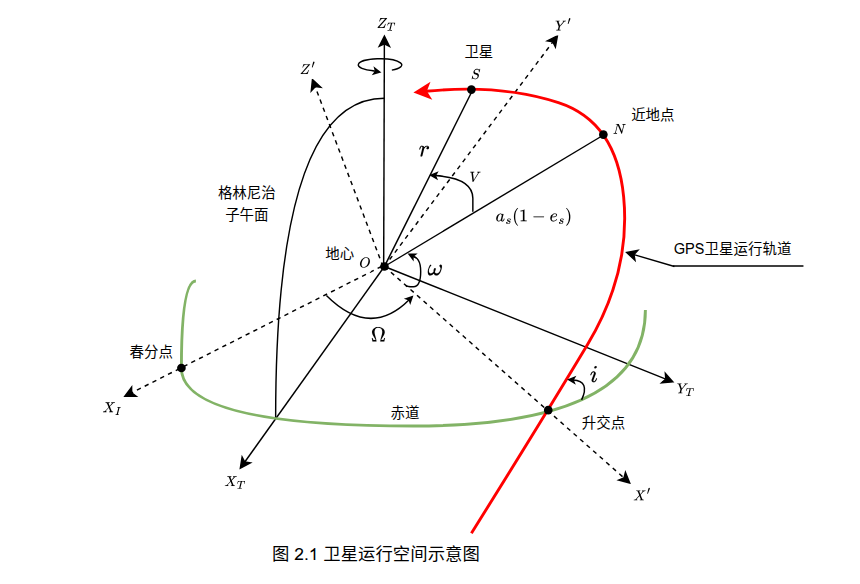
这里涉及三个坐标系:
- 卫星轨道平面坐标系
- 地心惯性坐标系(ECI): $X_{I}$ 指向春分点,和地球自转无关
- 地心地固坐标系(ECEF): 随地球自转 ,表示为 $(X_{T},Y_{T},Z_{T})$
- WGS84坐标系: WGS84 以经度、纬度、高程来描述位置, ECEF 是WGS84 的 笛卡尔坐标实现形式
这样我们转换的顺序为: 轨道平面 -> ECI -> ECEF -> WGS84
$$r_{ECI} = R_{z}(-\Omega) \cdot R_{x}(-i) \cdot R_{z}(-\omega) \cdot r_{轨道平面}$$
接着:
$$r_{ECEF} = R_{z}(-\theta_{G}) \cdot r_{ECI}$$
其中 $\theta_{G}$ 是 格林尼治恒星时(GMST) , 用于补偿地球自转,将惯性坐标”旋转”到随地球一起转动的地固系,在图 2.1 中表示为 $X_{I}$ 轴与 $X_{T}$ 轴对 $O$ 的夹角。
最后可以根据对应的公式替换为 WGS84 的 (经度,纬度,高程) , 这里不再赘述。
