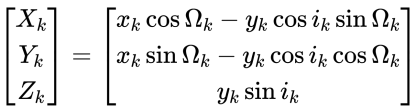一、星历参数
卫星在各种复杂因素的综合作用下,各个开普勒轨道参数不再是常数,卫星的实际运动轨道也会偏离无摄运动轨道,为了更加精确的描述卫星的实际运行轨道,GPS 采用了一套扩展的开普勒轨道参数,共计16个,这套轨道参数通常称为 星历参数 :
| 参数 | 描述 | 参数 | 描述 |
|---|---|---|---|
| $t_{oe}$ | 星历参考时间 | $\sqrt{a_{s}}$ | 卫星半长轴平方根 |
| $e_{s}$ | 轨道偏心率 | $i_{0}$ | $t_{oe}$时的轨道倾角 |
| $\Omega_{0}$ | 周内时等于0时的轨道升交点赤经 | $\omega$ | 轨道近地点角距 |
| $M_{0}$ | $t_{oe}$时的平近点角 | $\bigtriangleup n$ | 平均运动角速度校正值 |
| $\dot{i}$ | 轨道倾角对时间的变化率 | $\dot{\Omega}$ | 轨道升交点赤经对时间的变化率 |
| $C_{uc}$ | 升交点角距余弦调和校正振幅 | $C_{us}$ | 升交点角距正弦调和校正振幅 |
| $C_{rc}$ | 轨道半径余弦调和校正振幅 | $C_{rs}$ | 轨道半径正弦调和校正振幅 |
| $C_{ic}$ | 轨道倾角余弦调和校正振幅 | $C_{is}$ | 轨道倾角正弦调和校正振幅 |
这些数据是通过 理论方程推导 结合对精密观测数据的 长期拟合 最终确定,具体的推导太过繁琐,这里仅做了解。
二、长期摄动与短期摄动
| 特性 | 长期摄动 | 短期摄动 |
|---|---|---|
| 时间行为 | 持续、单调增长/减小(累计) | 周期性震荡(平均为零) |
| 数学形式 | 线性项或多项式项($k \cdot t,k \cdot t^{2}$) | 三角函数项($A \cdot \sin (B \cdot t+C)$) |
| 主要来源 | 地球扁率($J_{2}$) | 高阶引力项、日月引力、光压等 |
| 典型影响 | $\Omega,\omega,n$ 的漂移 | $a,e,i$ 的周期性波动 |
| 星历修正 | $\bigtriangleup n,\dot i,\dot \Omega$ | $C_{us},C_{uc},C_{rs},c_{rc},C_{is},C_{ic}$ |
三、位置计算
摄动力因素影响下的 GPS 卫星轨道参数示意图:
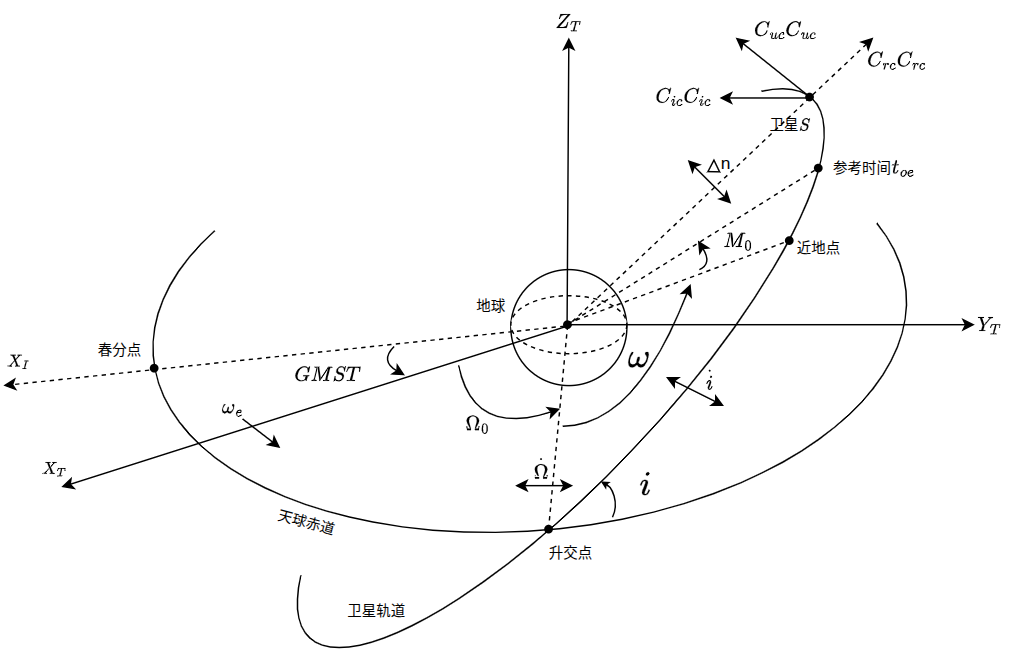
3.1 计算归化时间
卫星星历提供的轨道参数是以星历参考时间 $t_{oe}$ 为基准的,因此为了得到其余的轨道参数在 $t$ 时刻的值,就必须先求出 $t$ 时刻与参考时间 $t_{oe}$ 之间的差异,即
$$t_{k} = t - t_{oe}$$
对于有效星历而言,$t$ 应在 $t_{oe}$ 前后的两个小时之间,在实际计算中遵循如下步骤:
- 将观测时刻和星历参考时刻统一到同一时间系统并转换为周内秒。
- 计算两者差值 $\bigtriangleup t$。
- 通过加减一周(604800秒)的方式,将 $\bigtriangleup t$ 归化到 [-302400, 302400] 秒 的区间内,得到 $t_{k}$。
[-302400, 302400] 秒这个范围是基于 “周内秒” 系统 604800 秒的周期性而确定的。选择这个以 0 为中心、长度为一周的区间,可以确保通过简单的加减一周操作,将任何因跨越周边界而产生的 “巨大” 时间差,修正为反映真实物理时间间隔的 “最小” 时间差,从而保证卫星轨道计算的准确性和稳定性。
3.2 计算平均角速度
$$n = n_{0} + \bigtriangleup n$$
- $n_{0}$ : 根据参考半长轴 $a$ 计算的理论平均运动,$n_{0} = \sqrt{GM/a^{3}}$
- $\bigtriangleup n$ : 星历参数中的改正数,包含了地球非球形引力等长期摄动对平均运动的影响
3.3 计算平近点角
$$M_{k} = M_{0} +n \cdot t_{k}$$
如果所得的 $M$ 的值不在 $[0,2\pi]$ 之间,请务必加减 $2\pi$ 使 $M$ 落入这个区间中。
3.4 计算偏近点角
在得到平近点角 $M_{k}$ 和星历参数 $e_{s}$ 后,通常可以使用迭代法将偏近点角 $E_{k}$ 从开普勒方程中解出来。$E_{k}$ 的迭代初始值 $E_{0}$ 可置为 $M_{k}$ 。
$$E_{j} = M + e_{s} \sin(E_{j-1})$$
3.5 计算真近点角
将 $E_{k}$ 和 $e_{s}$ 代入 卫星的无摄运动轨道分析 一文中 2.4 节推导的公式中进行计算
3.6 计算升交点角距
将星历中给出的 $\omega$ 代入如下式:
$$\phi_{k} = v_{k} + \omega$$
升交点角距 $\phi _{k}$ 是卫星当前位置点 $S$ 与升交点相对于地心 $O$ 的夹角。
3.7 计算调和校正参数
计算公式如下,其中 $\delta u_{k}$ 表示升交点角距的摄动量, $\delta r_{k}$ 表示卫星矢径(卫星与地心的距离)摄动量,$\delta i_{k}$ 表示轨道倾角的摄动量:
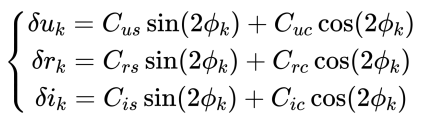
3.8 计算升交点角距/矢径/轨道倾角
加上调和校正参数:
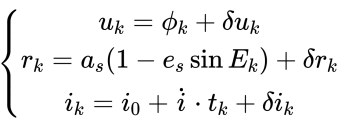
3.9 计算轨道平面坐标
在轨道平面直接坐标系中,卫星的位置是:
$$x_{k} = r_{k}\cos u_{k} \\ y_{k} = r_{k}\sin u_{k}$$
3.10 计算观测时刻经度
这里需要说明观测时刻的升交点经度 $\Omega_{k}$ 是该时刻升交点赤经 $\Omega$ 与格林尼治恒星时(GMST) 之间的差值,即:
$$\Omega_{k} = \Omega - GMST$$
且知:
$$\Omega = \Omega_{oe} + \dot\Omega t_{k}$$
其中,$\Omega$ 代表观测时刻的升交点赤经; $\Omega_{oe}$ 代表参考时刻 $t_{oe}$ 的升交点赤经; $\dot\Omega$ 代表升交点赤经的变化率,一般为每小时千分值几度;
卫星电文仅提供一个星期的开始时刻 $t_{w}$ (星期六午夜星期日子夜的交换时刻) 的格林尼治恒星时 $GMST_{w}$ 。因地球自转, $GMST$ 随之而不断增值,其增值速率为地球自转的速率 $w_{e}$ ,所以观测时刻的格林尼治恒星时为:
$$GMST = GMST_{w} + w_{e}t$$
$w_{e}$ 已知,$t$ 为观测时刻。
结合上式可得:
$$\Omega_{k} = \Omega_{oe} + \dot\Omega t_{k} -GMST_{w} - w_{e}t$$
令 $\Omega_{0} = \Omega_{oe} - GMST_{w}$ ,则可得:
$$\Omega_{k} = \Omega_{0} + \dot\Omega t_{k} - w_{e}t = \Omega_{0}+\dot\Omega (t-t_{oe}) - w_{e}t \\ = \Omega_{0} +(\dot \Omega - w_{e})t_{k} - w_{e}t_{oe}$$
3.11 计算在WGS84中的位置
在 卫星轨道平面坐标与WGS84转换 一文中详细介绍了轨道平面坐标与 WGS84 坐标系的转换,但是和本章不同的是,本章中轨道平面坐标系并不是以近地点与地心的连线作为 $X$ 轴,而是以地心与升交点的连线作为 $X$ 轴,因此在转换坐标系时略有不同:
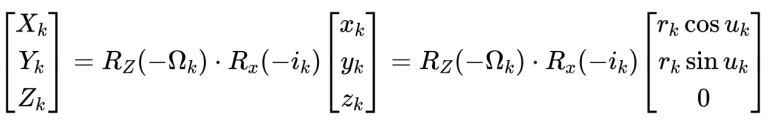
由上式可知卫星的在轨位置为: