一、概念介绍
倘若我们用5把尺子来测量一条线段的长度,由于工艺、材质等的不同,测量值会有不同,测量值如下所示(不同颜色指代不同尺子):

一般来说,会取平均值来做线段的长度:
$$\bar{x} = \frac{10.2+10.3+9.8+9.9+9.8}{5} = 10$$
但是这样做有道理吗?用其他的比如中位数可以吗?现在我们换个思虑来思考这个问题:
首先将测量值画到笛卡尔坐标系中,分别记作$y_{i}$;其次把猜测的值用平行于横轴的直线来表示,记作$y$;每个点都向$y$做垂线,垂线的长度就是$|y-y_{i}|$,也可以理解为测量值和真实值之间的误差,如下图所示:
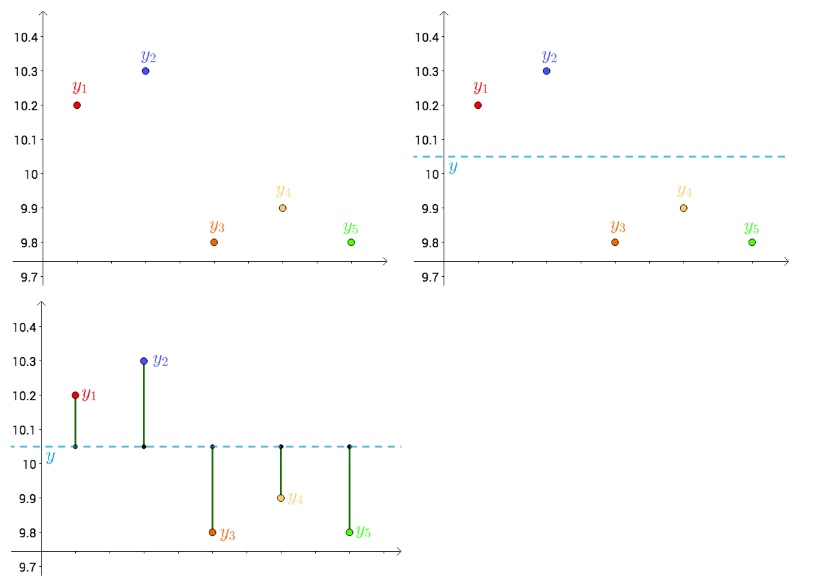
因为误差是长度,还要取绝对值,计算比较麻烦,因为可以使用平方来代替误差,那么总的误差的平方就是:
$$|y-y_{i}| \to (y-y_{i})^2 \ \ \ \ \Rightarrow \epsilon = \sum (y-y_{i})^2$$
因为$y$是猜测的,所以可以不断的变换的,自然总的误差$\epsilon$也是不断变换的。
法国数学家,阿德里安-馬里·勒讓德(1752-1833)提出让总的误差的平方最小的$y$就是真值,这是基于如果误差是随机的,应该围绕真值上下波动,这就是最小二乘法,即:
$$\epsilon = \sum (y-y_{i})^2最小 \Rightarrow 真值y$$
这是一个二次函数 ,对其求导,导数为0时取得最小值:
$$\frac{\mathrm{d} \epsilon }{\mathrm{d} y} = \frac{\mathrm{d} \sum (y-y_{i})^2}{\mathrm{d} y} = 2\sum (y-y_{i}) \\ = 2((y-y_{1})+(y-y_{2})+(y-y_{3})+(y-y_{4})+(y+y_{5})) = 0$$
进而:
$$5y = y_{1}+y_{2}+y_{3}+y_{4}+y_{5} \Rightarrow y = \frac{y_{1}+y_{2}+y_{3}+y_{4}+y_{5}}{5}$$
正好是算数平均值。最小二乘法,所谓“二乘”就是平方的意思。
二、最小二乘法的工程实践
在卫星伪距测量原理一文中,我们推导出了要想实现GPS伪距定位,则至少需要4颗卫星,可事实上通常接收机能接收到的卫星数多于4颗,这导致系统是超定的(方程数>未知数),也就是说我们无法找到一个解满足所有的方程,但是我们通过最小二乘法可以找到一个最优解,即在牛顿迭代法中提及的:
$$F(X+\bigtriangleup X) \approx F(X) + J\bigtriangleup X$$
我们的目标是让让修正后的新状态$X+\bigtriangleup X$满足$F(X+\bigtriangleup X)=0$(即所有残差为0),所以我们希望
$$F(X) + J\bigtriangleup X = 0$$
但是由于测量存在噪声、线性化有近似误差、卫星数通常多于4颗,这个方程往往没有精确解,我们找不到一个$\bigtriangleup X$能让上面这个等式对所有卫星都严格成立,因此我们的策略从"必须等于0"变成了"尽量等于0";我们将$F(X) + J\bigtriangleup X$当做一个误差向量(残差向量)$S$
$$S=F + J\bigtriangleup X $$
这个向量的每一个分量都代表了对应那个卫星的残差在本次修正后还剩下多少。则根据最小二乘法可有
$$S = |F + J\bigtriangleup X|^{2} = (F + J\bigtriangleup X)^{T}(F + J\bigtriangleup X)$$
此时对$S$关于$\bigtriangleup X$求导并令导数为0,即可得到正规方程:
$$J^{T}J\bigtriangleup X = -J^{T}F$$
解得:
$$\bigtriangleup X = -(J^{T}J)^{-1}J^{T}F$$
所以在牛顿迭代法中修正量应当替换为此处的表达式
在实际的GPS接收机中,不同卫星的测量质量是不同的,例如:
- 低仰角的卫星信号容易受到多路径效应和大气延迟的影响,测量误差较大
- 高仰角的卫星信号通常更”干净”,测量更可靠
因此在实际的计算中,为了提高定位精度,通常使用加权最小二乘法,其核心思想是给更可靠的测量值赋予更高的权重,让它们在最终的解中占据更大的“话语权”:
设权重矩阵$W$是一个$n*n$的对角阵,其对角元素$w_{i}$表示第$i$颗卫星伪距测量的权重,此时最小化的目标函数变为:
$$S_{w} = (F + J\bigtriangleup X)^{T}W(F + J\bigtriangleup X)$$
求解可得加权最小二乘解:
$$\bigtriangleup X = -(J^{T}WJ)^{-1}J^{T}WF$$
